图的着色
点着色¶
(讨论的是无自环无向图)
对无向图顶点着色,且相邻顶点不能同色。若 G 是 \(k\)- 可着色的,但不是 \((k-1)\)- 可着色的,则称 k 是 G 的色数,记为 \(\chi(G)\)。
对任意图 G,有 \(\chi(G) \leq \Delta(G) + 1\),其中 \(\Delta(G)\) 为最大度。
Brooks 定理¶
设连通图不是完全图也不是奇圈,则 \(\chi(G) \leq \Delta(G)\)。
证明¶
证明
设 \(|V(G)|=n\),考虑数学归纳法。
首先,\(n\leq 3\) 时,命题显然成立。
接下来,假设对于 \(n-1\) 时的命题成立,下面我们要逐步强化命题。
不妨只考虑 \(\Delta(G)\)- 正则图,因为对于非正则图来说,可以看作在正则图里删去一些边构成的,而这一过程并不会影响结论。
对于任意不是完全图也不是奇圈的正则图 G,任取其中一点 v,考虑子图 \(H:=G-v\),由归纳假设知 \(\chi(H)\leq\Delta(H)=\Delta(G)\),接下来我们只需证明在 H 中插入 v 不会影响结论即可。
令 \(\Delta:=\Delta(G)\),设 H 染的 \(\Delta\) 种颜色分别为 \(c_1,c_2,\dots,c_{\Delta}\),v 的 \(\Delta\) 个邻接点为 \(v_1,v_1,\dots,v_{\Delta}\)。不妨假设 v 的这些邻接点颜色两两不同,否则命题得证。
接下来我们设所有在 H 中染成 \(c_i\) 或 \(c_j\) 的点以及它们之间的所有边构成子图 \(H_{i,j}\)。不妨假设任意 2 个不同的点 \(v_i\),\(v_j\) 一定在 \(H_{i,j}\) 的同一个连通分量中,否则若在两个连通分量中的话,可以交换其中一个连通分量所有点的颜色,从而 \(v_i\),\(v_j\) 颜色相同。
这里的交换颜色指的是若图中只有两种颜色 a,b,那么把图中原来染成颜色 a 的点全部染成颜色 b,把图中原来染成颜色 b 的点全部染成颜色 a。
我们设上述连通分量为 \(C_{i,j}\),那么 \(C_{i,j}\) 一定只能是 \(v_i\) 到 \(v_j\) 的路。因为 \(v_i\) 在 H 中的度为 \(\Delta-1\),所以 \(v_i\) 在 H 中的邻接点颜色一定两两不同,否则可以给 \(v_i\) 染别的颜色,从而和 v 的其他邻接点颜色重复,所以 \(v_i\) 在 \(C_{i,j}\) 中邻接点数量为 1,\(v_j\) 同理。然后我们在 \(C_{i,j}\) 中取一条 \(v_i\) 到 \(v_j\) 的路,令其为 P,若 \(C_{i,j}\ne P\),那么我们沿着 P 顺次给路上的点染色,设遇到的第一个度数大于 2 的点为 u,注意到 u 的邻接点最多只用了 \(\Delta-2\) 种颜色,所以 u 可以重新染色,从而使 \(v_i\),\(v_j\) 不连通。
然后我们不难发现,对任意 3 个不同的点 \(v_i\),\(v_j\),\(v_k\),\(V(C_{i,j})\cap V(C_{j,k})=\{v_j\}\)。
到这里我们对命题的强化工作就已经做完了。
接下来就很简单。首先,如果 v 的邻接点两两相邻,那么命题得证。不妨设 \(v_1\),\(v_2\) 不相邻,在 \(C_{1,2}\) 中取 \(v_1\) 的邻接点 w,交换 \(C_{1,3}\) 中的颜色。得到的新图中,\(w\in V(C_{1,2})\cap V(C_{2,3})\),矛盾。
至此命题证明完毕。
Welsh–Powell 算法¶
Welsh–Powell 算法是一种在 不限制最大着色数 时寻找着色方案的贪心算法。
对于无自环无向图 G,设 \(V(G):=\{v_1,v_2,\dots,v_n\}\) 满足。
\(\deg(v_i)\geq\deg(v_{i+1}),~\forall 1\leq i\leq n-1\)
按 Welsh–Powell 算法着色后的颜色数至多为 \(\max_{i=1}^n\min\{\deg(v_i)+1,i\}\), 该算法的时间复杂度为 \(O\left(n\max_{i=1}^n\min\{\deg(v_i)+1,i\}\right)=O(n^2)\)。
过程¶
- 将当前未着色的点按度数降序排列。
- 将第一个点染成一个未被使用的颜色。
- 顺次遍历接下来的点,若当前点和所有与第一个点颜色 相同 的点 不相邻,则将该点染成与第一个点相同的颜色。
- 若仍有未着色的点,则回到步骤 1, 否则结束。
示例如下:
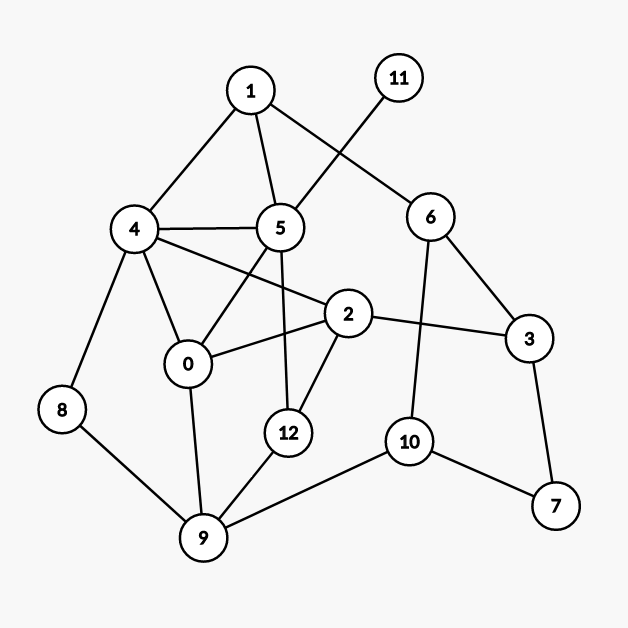
(由 Graph Editor 生成)
我们先对点按度数降序排序,得:
| 次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 点的编号 | 4 | 5 | 0 | 2 | 9 | 1 | 3 | 6 | 10 | 12 | 7 | 8 | 11 |
| 度数 | 5 | 5 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 1 |
| \(\min\{\deg(v_i)+1,i\}\) | 1 | 2 | 3 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 2 |
所以 Welsh–Powell 算法着色后的颜色数最多为 5。
另外因为该图有子图 \(C_3\), 所以色数一定大于等于 3。
-
第一次染色:
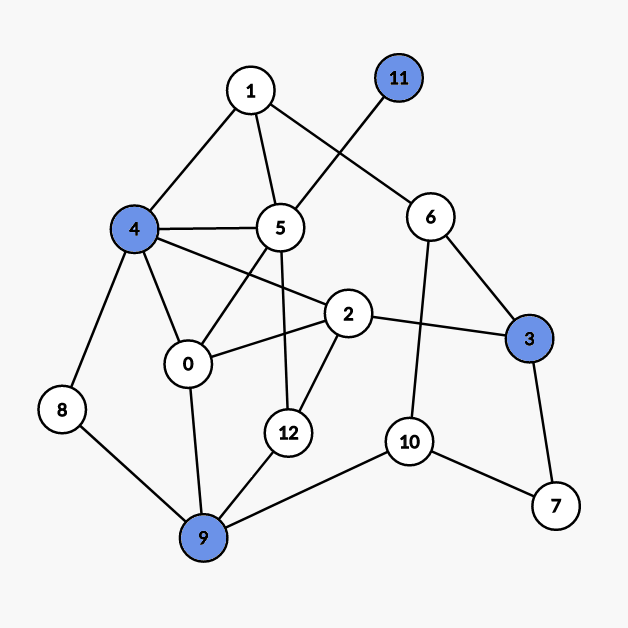
染
4 9 3 11号点。 - 第二次染色: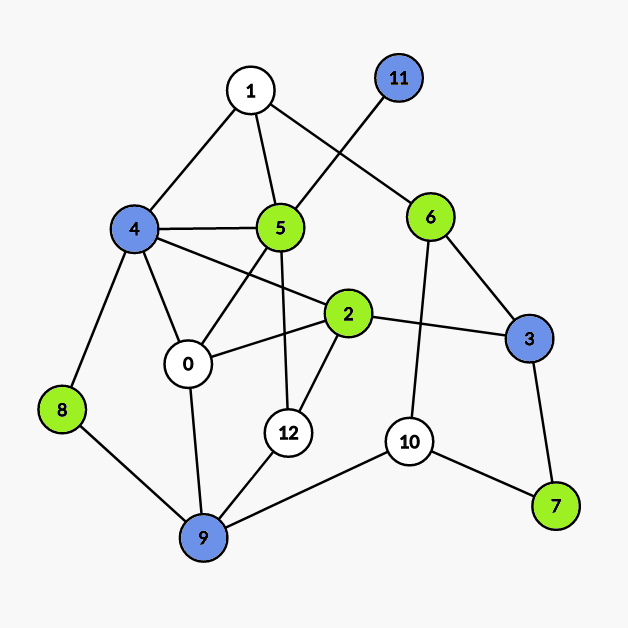
染
5 2 6 7 8号点。 - 第三次染色: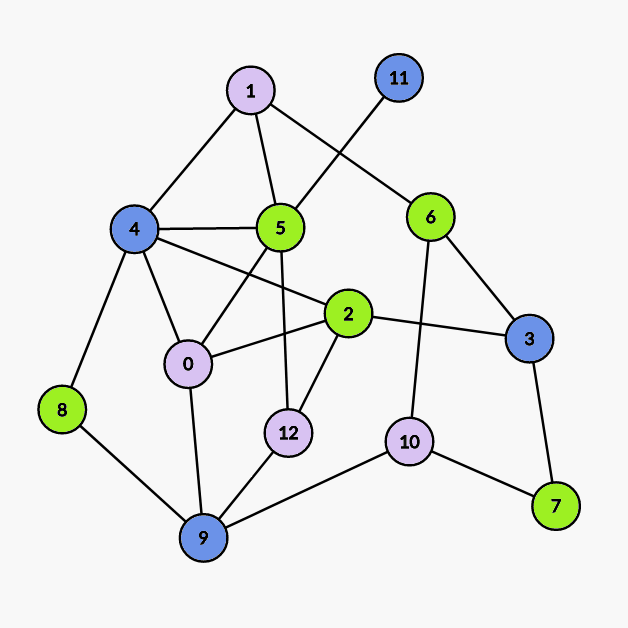
染
0 1 10 12号点。
证明¶
证明
对于无自环无向图 G,设 \(V(G):=\{v_1,v_2,\dots,v_n\}\) 满足
\(\deg(v_i)\geq\deg(v_{i+1}),~\forall 1\leq i\leq n-1\)
令 \(V_0=\varnothing\), 我们取 \(V(G)\setminus\bigcup_{i=0}^{m-1} V_i\) 中的子集 \(V_m\), 其中的元素满足
- \(v_{k_m}\in V_m\), 其中 \(k_m=\min\{k:v_k\notin\bigcup_{i=0}^{m-1} V_i\}\)
-
若
\(\{v_{i_{m,1}},v_{i_{m,2}},\dots,v_{i_{m,l_m}}\}\subset V_m,~i_{m,1}<i_{m,2}<\dots<i_{m,l_m}\)
则 \(v_j\in V_m\) 当且仅当
- \(j>i_{m,l_m}\)
- \(v_j\) 与 \(v_{i_{m,1}},v_{i_{m,2}},\dots,v_{i_{m,l_m}}\) 均不相邻
显然若将 \(V_i\) 中的点染成第 i 种颜色,则该染色方案即为 Welsh–Powell 算法给出的方案,显然有
- \(V_1\neq\varnothing\)
- \(V_i\cap V_j=\varnothing\iff i\neq j\)
- \(\exists \alpha(G)\in\Bbb{N}^*,\forall i>\alpha(G),~s.t.~ V_i=\varnothing\)
我们只需要证明:
\(\bigcup_{i=1}^{\alpha(G)} V_i=V(G)\)
其中
\(\chi(G)\leq\alpha(G)\leq\max_{i=1}^n\min\{\deg(v_i)+1,i\}\)
上式左边的不等号显然成立,我们考虑右边。
首先我们不难得出:
若 \(v\notin\bigcup_{i=1}^mV_i\),则 v 与 \(V_1,V_2,\dots,V_m\) 中分别至少有一个点相邻,从而有 \(\deg(v)\geq m\)
进而
\(v_j\in\bigcup_{i=1}^{\deg(v_j)+1}V_i\)
另一方面,基于序列 \(\{V_i\}\) 的构造方法,我们不难发现
\(v_j\in\bigcup_{i=1}^j V_i\)
两式结合即得证。
边着色¶
对无向图的边着色,要求相邻的边涂不同种颜色。若 G 是 k- 边可着色的,但不是 \((k-1)\)- 边可着色的,则称 k 是 G 的边色数,记为 \(\chi'(G)\)。
Vizing 定理¶
设 G 是简单图,则 \(\Delta(G) \leq \chi'(G) \leq \Delta(G) + 1\)
若 G 是二部图,则 \(\chi'(G)=\Delta(G)\)
当 \(n\) 为奇数(\(n \neq 1\))时,\(\chi'(K_n)=n\); 当 \(n\) 为偶数时,\(\chi'(K_n)=n-1\)
二分图 Vizing 定理的构造性证明¶
证明
按照顺序在二分图中加边。
我们在尝试加入边 \((x,y)\) 的时候,我们尝试寻找对于 \(x\) 和 \(y\) 的编号最小的尚未被使用过的颜色,假设分别为 \(l_x\) 和 \(l_y\)。
如果 \(l_x=l_y\) 此时我们可以直接将这条边的颜色设置为 \(l_x\)。
否则假设 \(l_x<l_y\), 我们可以尝试将节点 \(y\) 连出去的颜色为 \(l_x\) 的边的颜色修改为 \(l_y\)。
修改的过程可以被近似的看成是一条从 \(y\) 出发,依次经过颜色为 \(l_x,l_y,\cdots\) 的边的有限唯一增广路。
因为增广路有限所以我们可以将增广路上所有的边反色,即原来颜色为 \(l_x\) 的修改为 \(l_y\),原来颜色为 \(l_y\) 的修改为 \(l_x\)。
根据二分图的性质,节点 \(x\) 不可能为增广路节点,否则与最小未使用颜色为 \(l_x\) 矛盾。
所以我们可以在增广之后直接将连接 \(x\) 和 \(y\) 的边的颜色设为 \(l_x\)。
总构造时间复杂度为 \(O(nm)\)。
示例代码 UVa10615 Rooks
#include <iostream>
typedef char chr;
const int maxN = 100;
int t;
int n;
chr a[maxN + 10][maxN + 10];
int c[maxN + 10][maxN + 10];
int ans;
namespace graph {
struct Vertex {
int head;
int deg;
int vis[maxN + 10];
} vertex[2 * maxN + 10], e;
struct Edge {
int head;
int next;
int col;
} edge[2 * maxN * maxN + 10];
int ecnt;
void init() {
std::fill(c[0], c[0] + sizeof(c) / 4, 0);
for (int i = 1; i <= 2 * maxN; i++) vertex[i] = e;
for (int i = 0; i <= 2 * maxN * maxN; i++) edge[i].col = 0;
ecnt = 1;
ans = 0;
return;
}
void addEdge(int tail, int head) {
ecnt++;
edge[ecnt].head = head;
edge[ecnt].next = vertex[tail].head;
vertex[tail].head = ecnt;
vertex[tail].deg++;
return;
}
int get(int u) {
for (int i = 1; i <= n; i++)
if (!vertex[u].vis[i]) return i;
}
void DFS(int u, int ori, int upd) {
if (vertex[u].vis[ori] == 0) {
vertex[u].vis[upd] = 0;
return;
}
int e = vertex[u].vis[ori];
int v = edge[e].head;
DFS(v, upd, ori);
edge[e].col = upd;
edge[e ^ 1].col = upd;
vertex[u].vis[upd] = e;
vertex[v].vis[upd] = e ^ 1;
return;
}
void AddEdge(int u, int v) {
addEdge(u, v);
addEdge(v, u);
return;
}
void solve() {
for (int u = 1; u <= n; u++) {
for (int e = vertex[u].head; e; e = edge[e].next) {
int v = edge[e].head;
if (edge[e].col) continue;
int lu = get(u);
int lv = get(v);
if (lu < lv) DFS(v, lu, lv);
if (lu > lv) DFS(u, lv, lu);
int l = std::min(lu, lv);
vertex[u].vis[l] = e;
vertex[v].vis[l] = e ^ 1;
edge[e].col = l;
edge[e ^ 1].col = l;
}
}
}
void generate() {
for (int u = 1; u <= n; u++) {
for (int e = vertex[u].head; e; e = edge[e].next) {
int v = edge[e].head;
c[u][v - n] = edge[e].col;
}
}
return;
}
} // namespace graph
void mian() {
graph::init();
std::cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) std::cin >> a[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (a[i][j] == '*') graph::AddEdge(i, j + n);
for (int i = 1; i <= n * 2; i++) ans = std::max(ans, graph::vertex[i].deg);
graph::solve();
graph::generate();
std::cout << ans << '\n';
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) std::cout << c[i][j] << ' ';
std::cout << '\n';
}
return;
}
int main() {
std::cin >> t;
while (t--) mian();
return 0;
}
一道很不简单的例题 uoj 444 二分图
本题为笔者于 2018 年命制的集训队第一轮作业题。
首先我们可以发现答案下界为度数不为 k 倍数的点的个数。
下界的构造方法是对二分图进行拆点。
若 \(degree \bmod k \neq 0\), 我们将其拆为 \(degree/k\) 个度数为 k 的节点和一个度数为 \(degree \bmod k\) 的节点。
若 \(degree \bmod k = 0\), 我们将其拆为 \(degree/k\) 个度数为 k 的节点。
拆出来的点在原图中的意义相同,也就是说,在满足度数限制的情况下,一条边端点可以连接任意一个拆出来的点。
根据 Vizing 定理,我们显然可以构造出该图的一种 k 染色方案。
删边部分由于和 Vizing 定理关系不大这里不再展开。
有兴趣的读者可以自行阅读笔者当时写的题解。
色多项式¶
\(P(G,k)\) 表示 G 的不同 k 着色方式的总数。
\(P(K_n, k) = k(k-1)\cdots(k-n+1)\)
\(P(N_n, k) = k^n\)
在无向无环图 G 中,
- \(e=(v_i, v_j) \notin E(G)\),则 \(P(G, k) = P(G \cup e, k)+P(G\setminus e, k)\)
- \(e=(v_i, v_j) \in E(G)\),则 \(P(G,k)=P(G-e,k)-P(G\setminus e,k)\)
定理:设 \(V_1\) 是 G 的点割集,且 \(G[V_1]\) 是 G 的 \(|V_1|\) 阶完全子图,\(G-V_1\) 有 \(p(p \geq 2)\) 个连通分支,则:
\(P(G,k)=\frac{\Pi_{i=1}^{p}{(P(H_i, k))}}{P(G[V_1], k)^{p-1}}\)
其中 \(H_i=G[V_1 \cup V(G_i)]\)
参考资料¶
- Graph coloring - Wikipedia
- Welsh, D. J. A.; Powell, M. B. (1967), "An upper bound for the chromatic number of a graph and its application to timetabling problems", The Computer Journal, 10 (1): 85–86