图匹配
匹配 或是 独立边集 是一张图中没有公共边的集合。 在二分图中求匹配等价于网路流问题。
图匹配算法是信息学竞赛中常用的算法,总体分为最大匹配以及最大权匹配,先从二分图开始介绍,在进一步提出一般图的作法。
图的匹配¶
在图论中,假设图 \(G=(V,E)\),其中 \(V\) 是点集,\(E\) 是边集。
一组两两没有公共点的边集 \((M(M\in E))\) 称为这张图的 匹配。
定义匹配的大小为其中边的数量 \(|M|\),其中边数最大的 \(M\) 为 最大匹配。
当图中的边带权的时候,边权和最大的为 最大权匹配。
匹配中的边称为 匹配边,反之称为 未匹配边。
一个点如果属于 \(M\) 且为至多一条边的端点,称为 匹配点,反之称为 未匹配点。
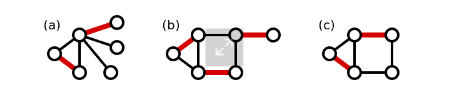
- maximal matching:无法再增加匹配边的匹配。不见得是最大匹配。
- 最大匹配(maximum matching):匹配数最多的匹配。
- 完美匹配(perfect matching):所有点都属于匹配,同时也符合最大匹配。
-
近完美匹配(near-perfect matching):发生在图的点数为奇数,刚好只有一个点不在匹配中,扣掉此点以后的图称为 factor-critical graph。
maximal matching
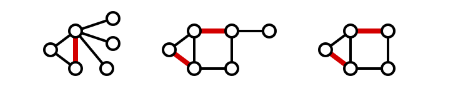
最大匹配
二分图匹配¶
一张二分图上的匹配称作二分匹配
设 \(G\) 为二分图,若在 \(G\) 的子图 \(M\) 中,任意两条边都没有公共节点,那么称 \(M\) 为二分图 \(G\) 的一个匹配,且 \(M\) 的边数为匹配数。
完美匹配¶
设 \(G=\langle V_1, V_2, E \rangle\) 为二分图,\(|V_1| \leq |V_2|\),\(M\) 为 \(G\) 中一个最大匹配,且 \(|M|=|V_1|\),则称 \(M\) 为 \(V_1\) 到 \(V_2\) 的完美匹配。
霍尔定理¶
设二分图 \(G=\langle V_1, V_2, E \rangle, |V_1| \leq |V_2|\),则 \(G\) 中存在 \(V_1\) 到 \(V_2\) 的完美匹配当且仅当对于任意的 \(S \subset V_1\),均有 \(|S|\leq|N(S)|\),其中 \(N(S)=\Cup_{v_i \in S}{N(V_i)}\),是 \(S\) 的邻域。
最大匹配¶
寻找二分图边数最大的匹配称为最大匹配问题。
算法¶
组合优化中的一个基本问题是求 最大匹配(maximum matching)。
二分图最大匹配¶
详见 二分图最大匹配 页面。
在无权二分图中,Hopcroft–Karp 算法可在 \(O(\sqrt{V}E)\) 解决。
二分图最大权匹配¶
详见 二分图最大权匹配 页面。
在带权二分图中,可用 Hungarian 算法解决。 如果在最短路搜寻中用 Bellman–Ford 算法,时间复杂度为 \(O(V^2E)\), 如果用 Dijkstra 算法或 Fibonacci heap,可用 \(O(V^{2}\log {V}+VE)\) 解决。
一般图最大匹配¶
详见 一般图最大匹配 页面。
无权一般图中,Edmonds' blossom 算法可在 \(O(V^2E)\) 解决。
一般图最大权匹配¶
详见 一般图最大权匹配 页面。
带权一般图中,Edmonds' blossom 算法可在 \(O(V^2E)\) 解决。
