Stern–Brocot 树与 Farey 序列

连分数的树¶

有两种主要方法，可以将所有可能的连分数，合并为有用的树结构。

Stern–Brocot 树¶

定义¶

Stern–Brocot 树是一种维护分数的优雅的结构，包含所有不同的正有理数。这个结构由 Moritz Stern 在 1858 年和 Achille Brocot 在 1861 年发现。

解释¶

Stern–Borcot 树从两个简单的分数开始：

这个 \(\frac{1}{0}\) 可能看得你有点懵逼。不过我们不讨论这方面的严谨性，你只需要把它当作 \(\infty\) 就行了。

每次在相邻的两个分数 \(\frac{a}{b},\frac{c}{d}\) 中间插入一个分数 \(\frac{a+c}{b+d}\)，这样就完成了一次迭代，得到下一个序列。于是它就会变成这样

既然称它为 Stern–Brocot 树，那么它总得有一个树的样子。来一张图：

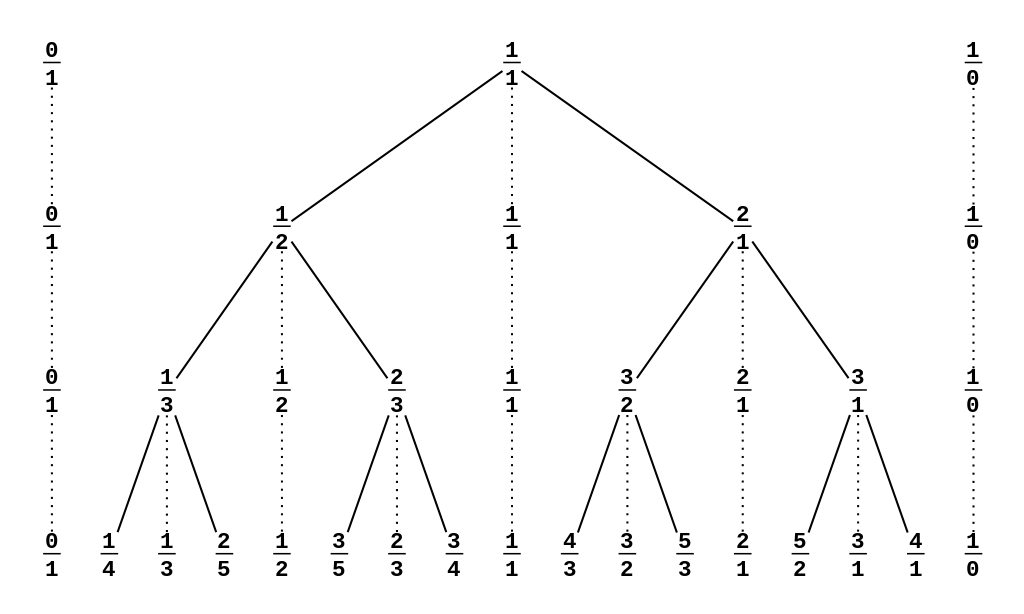
可以把第 \(i\) 层的序列当作是深度为 \(i-1\) 的 Stern–Brocot 树的中序遍历。

性质¶

接下来讨论 Stern–Brocot 树的性质。

单调性¶

在每一层的序列中，真分数是单调递增的。

略证：只需要在 \(\frac{a}{b}\le \frac{c}{d}\) 的情况下证明

就行了。这个很容易，直接做一下代数变换即可

另一边同理可证。

最简性¶

序列中的分数（除了 \(\frac{0}{1},\frac{1}{0}\)）都是最简分数。

略证：为证明最简性，我们首先证明对于序列中连续的两个分数 \(\frac{a}{b},\frac{c}{d}\)：

显然，只需要在 \(bc-ad=1\) 的条件下证明 \(\frac{a}{b}, \frac{a+c}{b+d}, \frac{c}{d}\) 的情况成立即可。

后半部分同理。证明了这个，利用扩展欧几里德定理，如果上述方程有解，显然 \(\gcd(a,b)=\gcd(c,d)=1\)。这样就证完了。

有了上面的证明，可以证明 \(\frac{a}{b}<\frac{c}{d}\)。

有了这两个性质，就可以把它当成一棵平衡树来做了。建立和查询就向平衡树一样做就行了。

连分数表示与父子节点¶

递推 \(\frac{p_k}{q_k}=\frac{a_k p_{k-1} + p_{k-2}}{a_k q_{k-1} + q_{k-2}}\)，意味着连分数表示对树中 \(\frac{p_k}{q_k}\) 的路径进行编码。要查找 \([a_0; a_1, \dots, a_{k}, 1]\)，必须使 \(a_0\) 向右移动，\(a_1\) 向左移动，\(a_2\) 向右移动等等，直到 \(a_k\)。

连分数节点 \([a_0; a_1, \dots, a_k,1]\) 的父节点是沿最后使用的方向后退一步获得的分数。

换句话说，当 \(a_k>1\) 时，它是 \([a_0; a_1, \dots, a_k-1,1]\)，而当 \(a_k=1\) 时，则是 \([a_0; a_1, \dots, a_{k-1}, 1]\)。

因此，\([a_0; a_1, \dots, a_k, 1]\) 的子节点是 \([a_0; a_1, \dots, a_k+1, 1]\) 和 \([a_0; a_1, \dots, a_k, 1, 1]\)。

索引¶

为 Stern Brocot 树编制索引。根顶点被分配了一个索引 \(1\)。然后，对于顶点 \(v\)，通过将 \(v\) 的前导位从 \(1\) 更改为 \(10\) 来分配其左子节点的索引，对于右子节点，通过将前导位从 \(1\) 更改为 \(11\) 来分配索引：

在这种索引中，连分数表示规定了有理数的 游程长度编码（run-length encoding）。

对于 \(\frac{5}{2} = [2;2] = [2;1,1]\)，其索引为 \(1011_2\)，其游程长度编码（考虑按升序排列的位）为 \([2;1,1]\)。

另一个例子是 \(\frac{2}{5} = [0;2,2]=[0;2,1,1]\)，其索引为 \(1100_2\)，其游程编码实际上为 \([0;2,2]\)。

值得注意的是，Stern–Brocot 树实际上是一个堆。也就是说，它是 \(\frac{p}{q}\) 的二叉树，它也是 \(p\) 和 \(q\) 的堆。

实现¶

构建实现

void build(int a = 0, int b = 1, int c = 1, int d = 0, int level = 1) {
  int x = a + c, y = b + d;
  // ... output the current fraction x/y
  // at the current level in the tree
  build(a, b, x, y, level + 1);
  build(x, y, c, d, level + 1);
}

def build(a = 1, b = 1, c = 1, d = 0, level = 1):
    x = a + c; y = b + d
    # ... output the current fraction x/y
    # at the current level in the tree
    build(a, b, x, y, level + 1)
    build(x, y, c, d, level + 1)

查询实现

string find(int x, int y, int a = 0, int b = 1, int c = 1, int d = 0) {
  int m = a + c, n = b + d;
  if (x == m && y == n) return "";
  if (x * n < y * m)
    return 'L' + find(x, y, a, b, m, n);
  else
    return 'R' + find(x, y, m, n, c, d);
}

def find(x, y, a = 0, b = 1, c = 1, d = 0):
    m = a + c; n = b + d
    if x == m and y == n:
        return ""
    if x * n < y * m:
        return 'L' + find(x, y, a, b, m, n)
    else:
        return 'R' + find(x, y, m, n, c, d)

例题¶

# check if a < b assuming that a[-1] = b[-1] = infty and a != b
def less(a, b):
    a = [(-1)**i*a[i] for i in range(len(a))]
    b = [(-1)**i*b[i] for i in range(len(b))]
    return a < b

# [a0; a1, ..., ak] -> [a0, a1, ..., ak-1, 1]
def expand(a):
    if a: # empty a = inf
        a[-1] -= 1
        a.append(1)
    return a

# return a-eps, a+eps
def pm_eps(a):
    b = expand(a.copy())
    a.append(float('inf'))
    b.append(float('inf'))
    return (a, b) if less(a, b) else (b, a)

# finds lexicographically smallest (q, p)
# such that p0/q0 < p/q < p1/q1
def middle(p0, q0, p1, q1):
    a0 = pm_eps(fraction(p0, q0))[1]
    a1 = pm_eps(fraction(p1, q1))[0]
    a = []
    for i in range(min(len(a0), len(a1))):
        a.append(min(a0[i], a1[i]))
        if a0[i] != a1[i]:
            break
    a[-1] += 1
    p, q = convergents(a)
    return p[-1], q[-1]

    def solve():
    n = int(input())
    C = [0] * n
    J = [0] * n
    # p0/q0 < y/x < p1/q1
    p0, q0 = 0, 1
    p1, q1 = 1, 0
    fail = False
    for i in range(n):
        C[i], J[i] = map(int, input().split())
        if i > 0:
            A = C[i] - C[i-1]
            B = J[i] - J[i-1]
            if A <= 0 and B <= 0:
                fail = True
            elif B > 0 and A < 0: # y/x > (-A)/B if B > 0
                if (-A)*q0 > p0*B:
                    p0, q0 = -A, B
            elif B < 0 and A > 0: # y/x < A/(-B) if B < 0
                if A*q1 < p1*(-B):
                    p1, q1 = A, -B
    if p0*q1 >= p1*q0 or fail:
        return 'IMPOSSIBLE'

    p, q = middle(p0, q0, p1, q1)
    return str(q) + ' ' + str(p)

Calkin–Wilf 树¶

定义¶

在二叉树中组织连分数的一种更简单的方法是 Calkin–Wilf 树。

通常如下所示：

树的根节点为 \(\frac{1}{1}\)。然后，对于数字为 \(\frac{p}{q}\) 的顶点，其子节点为 \(\frac{p}{p+q}\) 和 \(\frac{p+q}{q}\)。

性质¶

与 Stern–Brocot 树不同，Calkin–Wilf 树不是二叉搜索树，因此不能用于执行有理二叉搜索。

在 Calkin–Wilf 树中，当 \(p>q\) 时，分数 \(\frac{p}{q}\) 的直接父节点为 \(\frac{p-q}{q}\)；当 \(p<q\) 时，为 \(\frac{p}{q-p}\)。

在 Stern–Brocot 树中使用了收敛的递归。为了得出连分数和 Calkin–Wilf 树之间的联系，应该使用完整商（complete quotients）的递归。如果 \(s_k = \frac{p}{q}\)，则 \(s_{k+1} = \frac{q}{p \mod q} = \frac{q}{p-\lfloor p/q \rfloor \cdot q}\)。

另一方面，当 \(p>q\) 时，在 Calkin–Wilf 树中重复从 \(s_k = \frac{p}{q}\) 到它的父节点，那么将以 \(\frac{p \mod q}{q} = \frac{1}{s_{k+1}}\) 结尾。如果继续这样做，将以 \(s_{k+2}\)，然后 \(\frac{1}{s_{k+3}}\) 等结尾。由此可以推断：

1. 当 \(a_0>0\) 时，Calkin–Wilf 树中 \([a_0; a_1, \dots, a_k]\) 的直接父节点为 \(\frac{p-q}{q}=[a_0 - 1; a_1, \dots, a_k]\)。
2. 当 \(a_0=0\) 且 \(a_1>1\) 时，其直接父节点为 \(\frac{p}{q-p} = [0; a_1 - 1, a_2, \dots, a_k]\)。
3. 当 \(a_0=0\) 且 \(a_1=1\) 时，其直接父节点为 \(\frac{p}{q-p} = [a_2; a_3, \dots, a_k]\)。

相应地，\(\frac{p}{q} = [a_0; a_1, \dots, a_k]\) 的子节点为

1. \(\frac{p+q}{q}=1+\frac{p}{q}\)，即 \([a_0+1; a_1, \dots, a_k]\)。
2. \(\frac{p}{p+q} = \frac{1}{1+\frac{q}{p}}\)，对于 \(a_0>0\)，它是 \([0, 1, a_0, a_1, \dots, a_k]\)；对于 \(a_0=0\)，则是 \([0, a_1+1, a_2, \dots, a_k]\)。

值得注意的是，如果以广度优先搜索顺序枚举 Calkin–Wilf 树的顶点（即，根有一个数字 \(1\)，而顶点 \(v\) 的子节点有相应的索引 \(2v\) 和 \(2v+1\)），Calkin–Welf 树中有理数的索引将与 Stern–Brocot 树中的索引相同。

因此，Stern–Brocot 树和 Calkin–Wilf 树的相同级别上的数字是相同的，但它们的排序通过 位反转排列（bit-reversal permutation）而不同。

Farey 序列¶

定义¶

Stern–Brocot 树与 Farey 序列有着极其相似的特征。第 \(i\) 个 Farey 序列记作 \(F_i\)，表示把分母小于等于 \(i\) 的所有最简真分数按大小顺序排列形成的序列。

显然，上述构建 Stern–Brocot 树的算法同样适用于构建 Farey 序列。因为 Stern–Brocot 树中的数是最简分数，因此在边界条件（分母）稍微修改一下就可以形成构造 Farey 序列的代码。可以认为 Farey 序列 \(F_i\) 是 Stern–Brocot 第 \(i-1\) 次迭代后得到的序列的子序列。

Farey 序列同样满足最简性和单调性，并且满足一个与 Stern–Brocot 树相似的性质：对于序列中连续的三个数 \(\frac ab,\frac xy,\frac cd\)，有 \(x=a+c,y=b+d\)。这个可以轻松证明，不再赘述。

由 Farey 序列的定义，可以得到 \(F_i\) 的长度 \(L_i\) 公式为：

中间分数¶

对于 \(0\leq n\leq a_{k+1}\)，记中间分数为

中间分数还包含这样的分数：

这些中间分数介于 \(\frac{p_{-1}}{q_{-1}}\) 与 \(\frac{p_0}{q_0}=a_0\) 之间。

对于给定的 \(k\)，第 \(0\) 个中间分数 \(F_{k,0}=\frac{p_{k-1}}{q_{k-1}}\) 与最后一个中间分数 \(F_{k,0}=\frac{p_{k-1}}{q_{k-1}}\) 是渐进分数。

对比上述表达式与

可以得到 \(F_{k,n}=\left[a_0,\ldots,a_k,n\right]\)。因此，中间分数也是某个连分数展开的渐进分数，中间分数表达式的分子分母也一定互素。

两个相邻中间分数的差为

对于确定的 \(k\)，中间分数随着 \(n\) 的增加递增或递减。

定理：对实数 \(x\) 与渐进分数 \(\frac{p_k}{q_k}\)，有

在使用中这个定理经常放缩一下。由于 \(q_k\leq q_{k+1}\)，有

右半部分 \(\left|x-\frac{p_k}{q_k}\right|<\frac{1}{{q_k}^2}\) 无需计算更高阶的渐进分数，很常用，即下文 Dirichlet 逼近定理的连分数证法。

Dirichlet 逼近定理¶

Dirichlet 逼近定理是说，对于任意的一个无理数 \(\theta\)，均能找到无穷个有理数逼近它，满足不等式：

\(\left|\frac{p}{q}-\theta\right|\leqslant\frac{1}{q^2}\)

由于任一实数 \(qx\) 到最近的整数距离不超过 \(\frac{1}{2}\)，显然存在整数 \(p\) 和 \(q\) 使得

Dirichlet 逼近定理将右侧优化到了 \(\frac{1}{q^2}\)。等价的写法，\(|qx-p|<\frac{1}{q}\) 总有解。

当 \(x\) 是无理数的时候，可以让渐进分数的分母任意大，\(|qx-p|\) 任意小。

另外还有瓦伦定理：实数 \(x\) 连续两个渐进分数至少有一个满足 \(\left|x-\frac{p}{q}\right|<\frac{1}{2q^2}\)，由瓦伦（Vahlen）在 1895 年证明。

另外还有伯雷尔定理：实数 \(x\) 连续两个渐进分数至少有一个满足 \(\left|x-\frac{p}{q}\right|<\frac{1}{\sqrt{5}q^2}\)，由伯雷尔（Borel）在 1903 年证明。

这个 \(\sqrt{5}\) 是最优的，在无理数为例如黄金分割 \(\frac{1+\sqrt{5}}{2}=\left[1,1,1,\ldots\right]\) 等连分数展开自某位起均为 \(1\) 的时候取等。这些后续的定理也同样表明，在 Dirichlet 逼近定理中的小于等于号事实上也可以是小于号。

另外还有定理：实数 \(x\) 连分数展开无穷项不小于 \(n\)，则存在无穷多渐进分数满足 \(\left|x-\frac{p}{q}\right|<\frac{1}{\sqrt{n^2+4}q^2}\)。这种条件的极端情形例如 \(\frac{n+\sqrt{n^2+4}}{2}=\left[n,n,n,\ldots\right]\)。

其他的，还有 Kronecker 逼近定理：

如果 \(\theta\) 为无理数，\(\alpha\) 为实数，则对任意正数 \(\varepsilon\), 存在整数 \(n\) 和整数 \(m\)，使得：

\(\left|n\theta−m−\alpha\right|<\varepsilon\)

Dirichlet 逼近定理和 Kronecker 逼近定理，都可以用抽屉原理来解决。事实上，正是 Dirichlet 为了解决 Pell 方程，研究有理数逼近条件，抽屉原理才在历史上被第一次正式提出。

当然，采用抽屉原理的证明可以发现，下文中提到的最佳逼近有理数列，每项满足定理中右边改成分母为一次式的不等式。

进一步有结论，渐进有理数列中，每一项均满足 Dirichlet 逼近定理的不等式。

最佳有理逼近¶

讨论如何用有理数「最佳地」逼近无理数，不妨假设无理数落入 \((0,1)\) 区间。

「最佳」一词的概念：选定的有理数必须保证，比它与无理数的距离更近的有理数，分母都比它大。不存在分母比它小的有理数，到给定无理数的距离更近。

最佳有理数：在 Farey 数列的某一行中，与给定无理数距离最近的那个有理数。

这个有理数可能在下面几行依旧与无理数「距离最近」，但一定有某一行，会找到一个新的有理数，与无理数距离更近。因此去重复后可以得到 最佳逼近有理数列，分母严格递增，距离递减。

更加严谨的叙述为：

对实数 \(x\) 和有理数 \(\frac{p}{q}\)，如果对于任意的整数 \(a\) 和整数 \(0<b\leq q\)，\(\frac{a}{b}\neq\frac{p}{q}\)，均有

则称 \(\frac{p}{q}\) 是 \(x\) 的一个最佳有理逼近。

比无理数大的称为上逼近，否则为下逼近。由于无理数和有理数之间一定有有理数，最佳逼近有理数列必然为若干个上逼近，之后若干个下逼近，交替进行的形式。

有结论：

渐进分数必然为最佳有理逼近。

偶项渐进分数全都是下逼近，奇项渐进分数全都是上逼近。渐进分数列是下上交错的逼近。

在最佳逼近有理数列中，渐进分数是下上关系改变之前的倒数第一个数。如果将最佳逼近有理数列都写成有限简单连分数，那么在渐进分数之后（下上关系改变之后），连分数长度加一。

例如，\([0,2,4,2]\) 是 \(\sqrt{6}\) 减去 \(2\) 的一个渐进分数。

那么它的渐进分数列是：

它的最佳逼近有理数列是：

从每个渐进分数（不包含）开始，到下一个渐进分数（包含）为止，同为上逼近，或同为下逼近。

在最佳逼近列中，每一个最佳分数是上一个最佳分数与再往前一个渐进分数的分子分母对应求和。

性质¶

定理：最佳有理逼近一定是中间分数。

它的逆定理并不成立，中间分数不一定是最佳有理逼近。

渐进分数的等价性质¶

实数 \(x\) 的渐进分数 \(\frac{p}{q}\) 等价于这样的一类分数：

对于任意的整数 \(a\) 和整数 \(0<b\leq q\)，\(\frac{a}{b}\neq\frac{p}{q}\)，均有

也就是

根据等价性，这可以直接作为渐进分数的另一个定义方法。这个性质比最佳逼近更加严格，因此根据这个性质，渐进分数必然为最佳逼近。

证明：

首先有 \(|q_kx-p_k|<\frac{1}{q_{k+1}}\)。对于一个非渐近分数的中间分数 \(F_{k,n}=\frac{a}{b}\)，有位置分布

于是有

即 \(|bx-a|\geq\frac{1}{q_{k+1}}\)。由于 \(b=nq_k+q_{k-1}>q_k\)，因此 \(F_{k,n}=\frac{a}{b}\) 劣于比它分母更小的 \(\frac{p_k}{q_k}\)。

接下来证明，满足这个条件的都是渐进分数。

首先，越高阶的渐近分数越靠近 \(x\)，具有严格单调性。如果有 \(s<k\)，就有 \(|q_sx-p_s|>|q_kx-p_k|\)。

这是因为 \(q_{k+1}\geq q_s+q_{s+1}\)，有

整理即为上式。

接下来找出分母为 \(q_k\) 的满足上述性质的数，并指出它是渐进分数。

在给定 \(b\) 的时候，\(\min |bx-a|\leq\frac{1}{2}\)，并且取到最小的 \(a\) 最多只有两个取值。

当 \(b\) 在范围 \(0<b\leq q_k\) 遍历的时候，将上述的最小值继续比较其中的最小值，并记取到最小值中的最小值的多个 \(b\) 中，最小的 \(b\) 为 \(b_0\)，对应的 \(a\) 为 \(a_0\)。

这里的 \(a_0\) 至多有两个，而事实上只有一个，可以证明其唯一性。唯一性的证明补在最后。

从上述选取方式可以看出 \(\frac{a_0}{b_0}\) 也满足定理的条件，因此它是一个渐进分数 \(\frac{p_s}{q_s}\)。

又根据严格单调性，在 \(s<k\) 时无法取到最小，只能有 \(s=k\)。

至此距离证毕只剩下 \(a_0\) 的唯一性。

如果给定 \(b_0\)，取到 \(|b_0x-a|\) 的 \(a\) 不唯一，而是相邻的两个数，只能有 \(|b_0x-a|=\frac{1}{2}\)。此时记较小的一个为 \(a_0\)。于是有

如果它们不互素，记 \(d=\gcd(2a_0+1, 2b_0)\geq 3\)，则有

使得 \(|b_1x-a_1|=|b_0x-a_0|=\frac{1}{2}\)。这与上述选取方式中 \(b_0\) 的最小性矛盾。

此时将有理数 \(x\) 做连分数展开，则最后一个渐进分数的分子分母就是

由于 \(a_N\geq 2\)，\(q_{N-2}\geq 1\)，得到 \(q_{N-1}<b_0\)。于是

此时有更小的 \(q_{N-1}\) 可以取到最小值，仍旧与上述 \(b_0\) 的选取方式矛盾。证毕。

勒让德判别法¶

对实数 \(x\) 与分数 \(\frac{p}{q}\)，如果有

则 \(\frac{p}{q}\) 一定是 \(x\) 的渐近分数。

勒让德判别法的原始形式更加复杂，由勒让德（Legendre）于 1797 年发表在他的专著中。

勒让德判别法的原始表述是一个等价关系，这里给出的形式相对简化与宽松，是一个渐进分数的充分条件而非必要条件。

本页面主要译自博文 Дерево Штерна-Броко. Ряд Фарея 与其英文翻译版 The Stern-Brocot Tree and Farey Sequences。其中俄文版版权协议为 Public Domain + Leave a Link；英文版版权协议为 CC-BY-SA 4.0。